The blob in all its glory:
 Twirl with your mouse
Twirl with your mouse
swirling both sides of a simple ellipsoid
|
Click on the snapshot to download the blob's stl file.
|

|
Octave Code:
# name of the blob
project = "blob14";
function w = f(x2,y2,z2,c,r,e)
x = (x2-c(1))/r(1); # do some simple scaling
y = (y2-c(2))/r(2);
z = (z2-c(3))/r(3);
w = (x/(38)).^2+(y/(90)).^4+(z/(16)).^2-1; # <<<<<<<<<<< THE BLOB FUNCTION
w = -w - 1.3./(1.0+(x/10).^2+((y+78)/4).^2).^2;
endfunction;
# do the scaling
c_outer = [0,0,0]; # center of ellipsoid for outer surface
r_outer = [1,1,1];# x,y,z radii for ellipsoid for outer surface
step = 4; # grid pitch in mm start with 4mm to see the shape quickly. Once you have it just right, change to 2mm for printing
xmin = -100;
xmax = 100;
ymin = -120;
ymax = 120;
zmin = -50;
zmax = 50;
# this is for distorting the grid before applying the function
# note that the undistorted grid will be used to make the stl file
# just set it to x3=x; y3=y; z3=z; if no warping is needed.
function [x3,y3,z3]= prewarp(x,y,z)
# default definitions of the two swirls
# Both swirls have axes parallel to the z axis
px1 = 30+8; py1 =20; # position of swirl 1
px2=-30-8; py2 = 20; # position of swirl 2
t1 = 12+1*8; # effective width of both swirls
angle1 = 3; # angle of swirl 1
angle2 = -3; # angle of swirl 2 ( in radians)
one_mat = 0*x+1;
an = angle1*(one_mat./(1.0+((x-px1)/t1).^2+((y-py1)/t1).^2));
an2 = angle2*(one_mat./(1.0+((x-px2)/t1).^2+((y-py2)/t1).^2));
x3 = px2+(x-px2).*cos(an2)-(y-py2).*sin(an2)+px1+(x-px1).*cos(an)-(y-py1).*sin(an)-x;
y3 = py2+(y-py2).*cos(an2)+(x-px2).*sin(an2)+py1+(y-py1).*cos(an)+(x-px1).*sin(an)-y;
z3 = z;
endfunction;
source("../octave/func2stl_v01.m"); # do all the calculations
GNU Octave
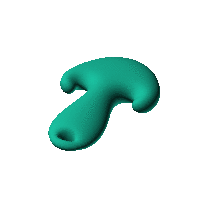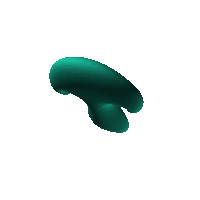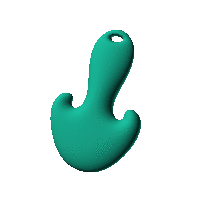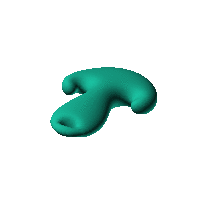
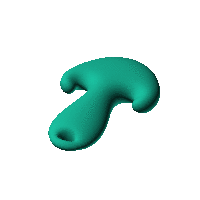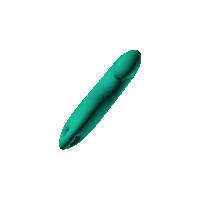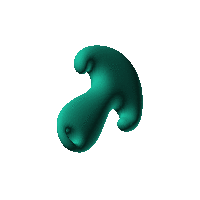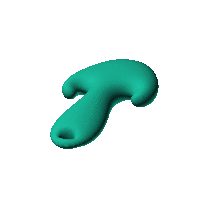
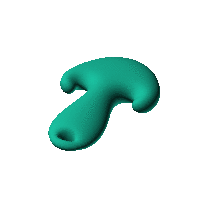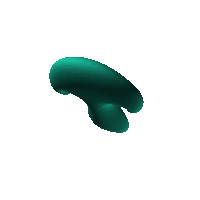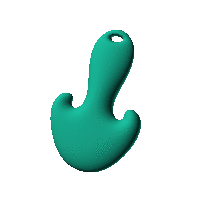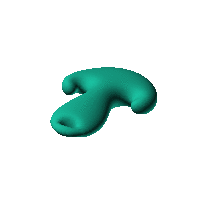
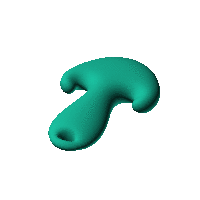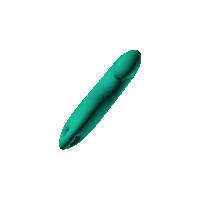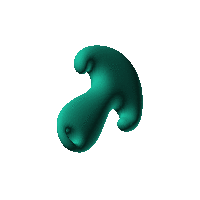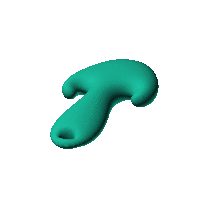
 Twirl with your mouse
Twirl with your mouse

